Производная

Теоретические основы математики

Элементы линейной и векторной алгебры

1. Матрицы
   1. Основные понятия о матрицах
   2. Действия над матрицами
2. Определители
   1. Определители второго порядка и их свойства
   2. Определители третьего порядка
   3. Определители n-го порядка
3. Обратная матрица
4. Системы линейных уравнений
   1. Основные понятия
   2. Формулы Крамера. Матричный способ решения систем линейных уравнений
   3. Решение систем линейных уравнений методом Гаусса
5. Элементы векторной алгебры
   1. Скалярные и векторные величины
   2. Линейные операции над векторами
   3. Угол между векторами. Проекция вектора на ось
   4. Линейная комбинация векторов. Базис
   5. Прямоугольная Декартова система координат
   6. Линейные операции над векторами, заданными в координатной форме
   7. Скалярное произведение векторов
   8. Векторное произведение векторов
   9. Смешанное произведение векторов

Учебно-методический комплекс составлен в соответствии с Государственным образовательным стандартом профессионального высшего образования РФ по дисциплине «Математика».

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Применение формул сокращенного умножения

1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.

$(a+b)^2=a^2+2ab+b^2$

2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

$(a-b)^2=a^2-2ab+b^2$

3. Разность квадратов раскладывается на произведение разности чисел и их сумму.

$a^2-b^2=(a+b)(a-b)$

4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.

$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.

$a^3+b^3=(a+b)(a^2-ab+b^2)$

7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.

$a^3-b^3=(a-b)(a^2+ab+b^2)$

Бесплатно

ЕГЭ.рф

Сайт: https://егэ.рф

Платформа бесплатного тестирования уровня подготовки школьников к ЕГЭ по математике базового и профильного уровней — на основе реальных заданий от ФИПИ 2021.

Первая часть экзамена будет проверена сразу после сдачи и ты увидишь свои результаты незамедлительно. Также ты сможешь получить детальный разбор ошибок в письменных заданиях от экспертов ЕГЭ.

А по итогу ты сможешь сопоставить свои результаты с проходными баллами в ВУЗы и выбрать, куда поступать.

«4ЕГЭ»

Сайт: https://4ege.ru

Каждый видеоурок состоит из двух основных частей: простое изложение самой важной и необходимой теории по заданной теме и решения основных задач ЕГЭ

«Синергия»

Сайт: https://synergy.ru

Для вашего удобства на сайте собрано все, что может потребоваться для подготовки к экзамену по математике:

• Демоверсии и КИМы, ЕГЭ предыдущих периодов
• Теория и практика по каждому типу задания
• Официальная информация и новости

Весь теоретический материал по математике разделен на вопросы из ЕГЭ и собран в файлы. Просто выбирайте интересующую тему (вопрос, раздел), открывайте лист и повторяйте (или учите, если забыли).

Информация изложена кратко, но просто и понятно. Схематическая подача поможет все быстро запомнить.

В практическом разделе собраны готовые решения самых сложных тестов. Просто выбирайте задание и смотрите подробный план решений задач того или иного типа.

Для удобства разбора листы разделены на 2 части. В первой — только сами задачи, которые можно решать самостоятельно. Во второй части — те же задачи, но с расписанным решением.

«РешуЕГЭ»

Сайт: https://mathb-ege.sdamgia.ru

Здесь регулярно выкладывают тренировочные варианты ЕГЭ по математике базового и профильного уровней. Каждый месяц — новый вариант. По окончании тестирования система проверит ваши ответы, покажет правильные решения и выставит оценку.

Чтобы тренироваться по определённым темам, вы можете составить свой вариант — по конкретным разделам задачного каталога.

Также на сайт размещен курс из 100 занятий «Д. Д. Гущин. Готовимся к ЕГЭ по профильной математике«. В нем рассмотрены все экзаменационные темы, дано большое количество заданий из школьной математики, материалов ЕГЭ, математических олимпиад и вузовских вступительных испытаний.

Занятия включают в себя конспекты, видеоуроки с разбором простых и сложных случаев, упражнения для мгновенной самопроверки и варианты для самостоятельной работы.

Для начала нужно авторизоваться на сайте и пройти входное тестирование, чтобы был построен ваш индивидуальный образовательный маршрут.

«Математика ЕГЭ 100БАЛЛОВ»

Сайт: https://vk.com

Страница для самоподготовки к ЕГЭ по математике волонтерского некоммерческого проекта. Ежедневно размещаются различные задания и полезные материалы для подготовки к экзамену по математике.

Есть теория в картинках, видеоуроки по отдельным темам, практические задания и пробные варианты ЕГЭ.

«Математикс»

Сайт: https://www.youtube.com

Канал создан в помощь тем, кто готовится к ЕГЭ по математике.

Здесь вы найдете плейлисты, посвященные следующим темам:

• Уравнениям и Неравенствам №13 и №15 ЕГЭ
• Задачам ЕГЭ №17 №18 №19
• Стереометрии и Планиметрии №14 и №16 ЕГЭ
• Высшей Математике (Теория с примерами)
• Разборам задач из вариантов Ларина
• Разборам вариантов СтатГрад

«ЕГЭ и ОГЭ на 80-ballov. Годограф»

Сайт: https://www.youtube.com

На ютуб-канале выложены короткие видеоуроки по основным темам подготовки «ЕГЭ по Математике 2021 80 баллов». Всего в плейлисте 261 видео. Для бесплатного просмотра открыто примерно 20% полного курса.

Полный курс, включающий в себя не только видеоматериал, доступен по платной подписке на сайте проекта 80-ballov.ru. Можно сначала оценить качество материала и подачи и, при необходимости, оплатить полный доступ.

Канал Бориса Трушина

Сайт: https://www.youtube.com

Личный канал преподавателя математики онлайн-школы «Фоксфорд».

Здесь вы найдете короткие и ёмкие видеоуроки по следующим темам:

• Задания 1-12. ЕГЭ. Математика. Профильный уровень
• Задания 13-19. ЕГЭ. Математика. Профильный уровень
• Разборы вариантов ЕГЭ
• Подборки по темам: Квадратный трёхчлен, Планиметрия, Неравенства, Теория вероятностей, Тригонометрия, Теория чисел и др.

Задания второй части профильного экзамена

В эту часть вошли непростые, комбинированные задачи, однако научиться решать можно каждую.

Задание №13 посвящено уравнениям: тригонометрическим, показательным и другим. Всё чаще в этом номере дают комбинаторное уравнение — логарифм плюс тригонометрия и другие вариации.

В задании №14 вам предлагается решить стереометрическую задачу. Она может быть на объём многогранников и их сечения или нахождение расстояния между прямой и плоскостью. Чтобы решить эти задачи, нужно хорошо знать теорию и много практиковаться. 

В задании №15 вам встретятся неравенства: смешанные, иррациональные или неравенства, содержащие модуль.

Для решения задачи №16 нужны твёрдые знания по планиметрии. Это задание проверяет ваше умение находить элементы трапеции, треугольника, окружности и других фигур. 

Задание №17 часто называют экономикой, так как оно связано с финансовой математикой. Вам может попасться задача о кредитах: например, на поиск суммы платежа, процентной ставки или срока. Также в этом номере вы можете встретить задачу на вклады или оптимизацию. Решение потребует большого количества вычислений, поэтому развивайте навык быстрого счёта.

Одно из самых сложных заданий ЕГЭ по профильной математике 2021 — №18. Это задача с параметром. В школе эту тему часто обходят стороной. Прежде чем приниматься за решение, нужно хорошо повторить функции, их свойства и графики.

Задание №19 — нестандартная задача, можно сказать, олимпиадного уровня. Она проверяет умение строить и исследовать простейшие математические модели. Вам помогут логика и хорошее знание математики в целом.

Виды заданий

В 2020 году госэкзамен содержит 19 заданий, которые делятся на два типа. Во-первых, это простые тесты, в которых надо выбрать правильный ответ. Его несложно увидеть на графике. Иногда нужно воспользоваться логикой.

Во-вторых, текстовые задачи. У них есть свои подклассы — вопросы, в которых достаточно расписать по всем правилам ход решения, дать ответ, и упражнения, где нужны не только примеры, но и строгое обоснование (теория, речь о № 18 и 19).

Важные моменты

Текстовых задач многие боятся. На самом же деле они такими уж страшными не являются для их решения нужно:

• вчитаться в суть условия и понять, что хочет видеть в ответе разработчик (80% успеха);
• применять алгоритм (не заученный порядок формул, а именно порядок рассуждений).

Сложность заключается в том, что некоторые учителя еще во время учебного года разбирают текстовые упражнения с учениками, давая готовое решение. Школьники, не особо вдаваясь в рассуждения о том, откуда что берется, заучивают формулировки и формулы. Этого делать не нужно, так легко запутаться. Создателям достаточно будет ввести в условие задачи незначительное изменение, чтобы весь заученный материал оказался бесполезным.

Где чаще всего совершают ошибки

Эксперты отмечают нередкие ошибки в первой части (которая решается элементарно). То ли в спешке, то ли из-за нервов, но ученики пишут скорость не того пешехода, путают плюс и минус. Поэтому привычка постоянно себя перепроверять может спасти вам десятки баллов.

Если идти по списку сложных вопросов, то:

• в № 11 следует внимательно читать условие и не путаться в единицах измерения;
• № 13 и 15 -знать формулы наизусть (первая неделя — учим, последняя — повторяем);
• № 14, 16 — не забудьте составить чертеж, он часто нужен по условию и нередко помогает проверять себя на правильность рассуждений;
• № 17 — применяем алгоритм, а не готовый порядок решения;
• № 19 — к ходу рассуждений добавляем теоретическое обоснование.

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Формулы приведения задаются в виде таблицы:

Обратные тригонометрические функции и простейшие тригонометрические уравнения

Арккосинус

Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.

Если, $|а|≤1$, то $arccos а = t ⇔ \{\table \cos (t)=a; \0≤t≤π;$

$arcos(-a) = π-arccos⁡a$, где $0≤а≤1$

Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение

$t=±arccos ⁡ a+2πk; k∈Z$

Частные случаи

$cos t =1, t = 2πk;k∈Z$

$cos t = 0, t = {π}/{2}+πk;k∈Z$

$cos t = -1, t=π+2πk;k∈Z$

Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$

$сos{2πx}/{3}=-{√3}/{2}$

${2πx}/{3}=±arccos⁡(-{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$

${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$

Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$

$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$

$x=±1,25+3k$

Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения

$k=0$

$x_1= -1,25$

$x_2=1,25$

$к=1$

$х_1=3-1,25=1,75$

$х_2=3+1,25=4,25$

Нам подходит $1,25$ – это и есть результат

Ответ: $1,25$

Арксинус

Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.

Если, $|а|≤1$, то $arcsin a = t ⇔ \{\table \sint=a; \-{π}/{2}≤t≤{π}/{2};$

$arcsin(-a)= — arcsin a$, где $0≤а≤1$

Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:

$1. t_1 = arcsin a+2πk;k∈Z$

$t_2 = (π- arcsin a)+ 2πk;k∈Z$

$2. t=(-1)^n arcsin ⁡ a+πn; n∈Z$

$3.$ Частные случаи

$sin t = 0, t=πk;k∈Z$

$sin t = 1, t={π}/{2}+2πk;k∈Z$

$sin t = -1,t=-{π}/{2}+2πk;k∈Z$

Арктангенс

$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.

$arctg a = t ⇔ \{\table \tgt=a; \-{π}/{2}≤t≤{π}/{2};$

$arctg(-a)= — arctg a$

Структура ЕГЭ по математике 2022

Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

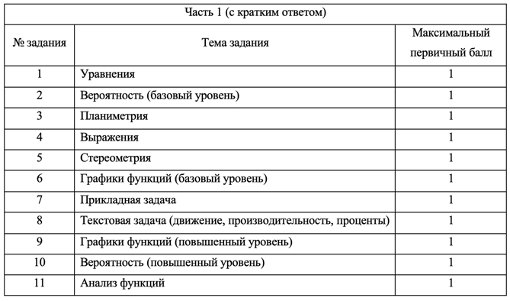
Темы заданий с кратким ответом, ЕГЭ по математике 2022, профиль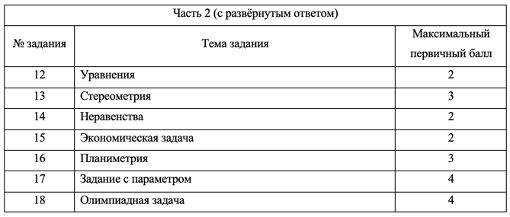
Темы заданий с развернутым ответом, ЕГЭ по математике 2022, профиль

Задания с кратким ответом принесут вам до 11 первичных баллов. Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов (что сейчас — мы еще не знаем). Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2.

Расскажем, как эффективно организовать подготовку к ЕГЭ,
на консультации

Подготовка к первой части экзамена по информатике

Внимательно читайте условие задачи. Большинство ошибок при выполнении заданий связано с неверным пониманием условия. Познакомьтесь с разными вариантами формулировки заданий. Помните о том, что незначительное изменение формулировки всегда приводят к ухудшению результатов экзамена.
Выучите наизусть таблицу степеней числа 2.
Помните о том, что Кбайты в задачах означают кибибайты, а не килобайты. 1 кибибайт = 1024 байта

Это поможет избежать ошибок при вычислениях.
Уделите особое внимание задачам № 9, 10, 11, 12, 15, 18, 20, 23. Именно эти задачи, согласно анализу результатов прошлых лет, особенно сложны

Сделайте на них упор при подготовке к ЕГЭ по информатике.

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

• $a$ — старший коэффициент;
• $b$ — средний коэффициент;
• $c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0   х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $33

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

1. найти общий знаменатель дробей, входящих в уравнение;
2. умножить обе части уравнения на общий знаменатель;
3. решить получившееся целое уравнение;
4. исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

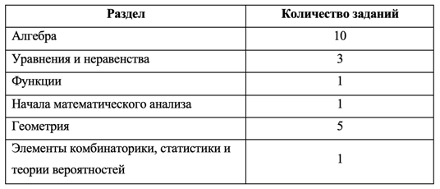
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Examer

Сайт — examer.ru/ege_po_matematike/2021/ Длительность обучения — индивидуально. Стоимость обучения — бесплатно для самостоятельной подготовки или 2 490 рублей в режиме Турбо с видеоуроками и разбором домашних заданий.

На этом ресурсе школьники могут готовиться только к экзамену профильного уровня. На Examer нет репетиторов или уроков как таковых. Здесь есть теория для самостоятельного изучения и задания для практической отработки. Можно заниматься дома, а можно — в любом удобном месте, поскольку у ресурса есть мобильные приложения для Android и iOS.

Существенный недостаток — отсутствие разборов заданий. Если у ребенка не получается решить какую-то задачу, с проблемой он будет разбираться самостоятельно. Для этого можно почитать теоретические материалы или воспользоваться поиском в интернете. Безусловный плюс ресурса — бесплатный доступ на неограниченной время. Это прекрасная возможность для ребят из малообеспеченных семей подтянуть свои знания по математике и подготовиться к ЕГЭ.

Перед началом обучения система попросит пройти тест на определение начального уровня знаний и предполагаемого результата ЕГЭ по математике. Затем для каждого в автоматическом режиме составляется индивидуальный план подготовки. Студент проходит модули последовательно. Каждый новый урок будет открыт после успешного решения задач по предыдущему.

Важно!
В бесплатном режиме возможности системы ограничены. Максимальную эффективность дает Турбокурс, в котором предусмотрено 12 видеоуроков в месяц

Домашние задания с проверкой преподавателя, тестирование, помощь в решении трудных задач.

Советы по подготовке к ЕГЭ по профильной математике 2021

Повторите теорию

Не откладывайте на потом. Вспомните все определения, формулы и понятия перед там, как приступать к решению задач. Попробуйте писать формулы по памяти, а потом сверять

И не забывайте: важно не вызубрить темы, а понять их. 

Не пропускайте первую часть

Одна из грубых ошибок — переходить сразу к решению второй части ЕГЭ. Многие задачи из первой решаются довольно просто, но не стоит их недооценивать. Они составлены так, чтобы проверить не только навык решения, но и внимательность к деталям. Прорабатывайте номера из первой части, ведь для достижения цели важен каждый балл. 

Внимательно читайте текст заданий

Смотрите, в каких единицах измерения требуется ответ и нужно ли его округлять

В задании №7 важно понимать, какой график вам дан — производной или функции. От этого зависит ответ на заданный вопрос

В экономической задаче №17 нельзя использовать готовую формулу. Вам нужно написать математическую модель самостоятельно.

Научитесь хорошо считать в уме

Учитесь вычислять без калькулятора — некоторые задания требуют навыка быстрого счёта. К тому же, на экзамене вам нужно оставить как можно больше времени на сложные задачи и проверку.

Проверяйте решения и ответы

Например, убедитесь, что правильно перевели число из обычной дроби в десятичную. Арифметические ошибки также часто встречаются в задаче на финансовую математику

В задании №9 обратите внимание на знаки, особенно если вам попались тригонометрические функции

Также важно без ошибок определить ограничения x в задаче №13. Если исходное уравнение содержит tgx, то — cosx≠0

Если уравнение содержит квадратный корень, подкоренное выражение — ≥0

Если исходное уравнение содержит tgx, то — cosx≠0. Если уравнение содержит квадратный корень, подкоренное выражение — ≥0.

Проверяйте свои знания

Вы можете пройти тест на бесплатном вводном занятии с преподавателем или на сайте ФИПИ. Так вы узнаете, что помните хорошо, а что нужно повторить. Также вы можете воспользоваться нашей библиотекой знаний с полезными материалами для подготовки. Нужно только зарегистрироваться на сайте. 

Не бойтесь второй части 

Смело решайте задания из второй части. Попробуйте справиться с заданиями №13 и №15. Скорее всего, они вам хорошо знакомы. Чаще всего №13 оказывается не таким уж и сложным. Если вы хорошо знаете геометрию, начните с №14 или №16. Если вам по душе алгебра, решайте задачи на параметр и свойства чисел — №18, 19.

Отдыхайте 

Составьте комфортное расписание занятий. Подготовка к ЕГЭ по профильной математике в 2021 не должна быть тяжким бременем. Проводите больше времени на свежем воздухе, встречайтесь с друзьями и не забывайте про здоровый сон. 

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Варианты математических олимпиад

Здесь содержатся варианты олимпиад по математике, используемые в повседневной работе. Ведь наилучший способ подготовиться к олимпиаде — это постоянно решать варианты последних лет.

Двузначное число в каждой ссылке означает год проведения финала олимпиады.

Всероссийская олимпиада школьников по математике

	ШЭ	МЭ	РЭ	ЗЭ
5 класс	, , , , ,	,	—	—
6 класс	, , , , ,	,	—	—
7 класс	, , , , ,	, , , , ,	—	—
8 класс	, , , , ,	, , , , ,	—	—
9 класс	, , , , ,	, , , , ,	, , , , ,	, , , ,
10 класс	, , , , ,	, , , , ,	, , , , ,	, , , , ,
11 класс	, , , , ,	, , , , ,	, , , , ,	, , , ,

Примечания.

• Муниципальный этап для 5 и 6 классов начиная с 2015/16 года не проводится.
• Региональный и заключительный этапы для 5–8 классов не предусмотрены. Вместо них проводится олимпиада им. Леонарда Эйлера (для восьмиклассников).

Олимпиада им. Леонарда Эйлера

Олимпиада им. Леонарда Эйлера («Всеросс в младшей лиге») проводится с 2008/09 года.

Регион	, , , , , , , , , ,
Финал	, , , , , , , , , ,

Олимпиада «Покори Воробьёвы горы!»

5–6 классы	, 20a, 20b, 18.1a, 18.1b, 18.2a, 18.2b, 18.3a, 18.3b17.1a, 17.1b, 17.2a, 17.2b, 17.3a, 17.3b16.1a, 16.1b, 16.2a, 16.2b, 16.3a, 16.3b
7 класс	, 20a, 20b, 18.1a, 18.1b, 18.2a, 18.2b, 18.3a, 18.3b17.1a, 17.1b, 17.2a, 17.2b, 17.3a16.1a, 16.1b, 16.2a, 16.2b, 16.3a, 16.3b , , ,
8 класс	, 20a, 20b, 18.1a, 18.1b, 18.2a, 18.2b, 18.3a, 18.3b17.1a, 17.1b, 17.2a, 17.2b, 17.3a16.1a, 16.1b, 16.2a, 16.2b, 16.3a, 16.3b , , ,
9 класс	, 20a, 20b, 18.1a, 18.1b, 18.2a, 18.2b, 18.3a, 18.3b17.1a, 17.1b, 17.2a, 17.2b, 17.3a16.1a, 16.1b, 16.2a, 16.2b, 16.3a, 16.3b , , ,
10–11 классы	, 20.10, 20.1119.1, 19.2, 19.3, 19.4, 19.5, 19.618.1, 18.2, 18.3, 18.4, 18.5, 18.617.1, 17.2, 17.3, 17.4, 17.516.1, 16.2, 16.3, 16.4, 16.5, 16.615.1, 15.2, 15.3, 15.4, 15.5, 15.614.1, 14.2, 14.3, 14.4, 14.5, 14.6, 14.713.1, 13.2, 13.3, 13.4, 13.5, 13.712.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.711.1, 11.2, 11.3, 11.410.1, 10.2, 10.3, 10.4, 10.5

Олимпиада «Физтех»

	Онлайн	Финал
5 класс	, ,	—
6 класс	, ,	—
7 класс	, , ,	—
8 класс	, , , ,	—
9 класс	, , , , , ,	20.1, 20.2;  19.1, 19.218.1, 18.2;  17.1, 17.216.1, 16.2, 16.3
10 класс	, , , , , ,	20.1, 20.2;  19.1, 19.218.1, 18.2;  17.1, 17.216.1, 16.2, 16.315.1, 15.2, 15.3
11 класс	, , , , , ,	20.1, 20.2;  19.1, 19.218.1, 18.2;  17.1, 17.216.1, 16.2, 16.315.1, 15.2, 15.314.1, 14.2;  13.1, 13.212.1, 12.2;  11.1, 11.210.1, 10.2;  09.1, 09.2;  ,
Экзамен1994 — 2008	08.1, 08.2, 08.3, 08.407.1, 07.2, 07.3, 07.406.1, 06.2, 06.3, 06.405.1, 05.2, 05.304.1, 04.2, 04.303.1, 03.2, 03.302.1, 02.2, 02.301.1, 01.2, 01.3	00.1, 00.299.1, 99.298.1, 98.297.1, 97.2, 97.396.1, 96.2, 96.395.1, 95.2, 95.394.1, 94.2, 94.3

Примечания.

• Очный финал для 5–8 классов пока не проводится.
• В 2016/17 и 2017/18 годах на онлайн-этапе для 5 и 6 классов давалось задание 7 класса.
• Очный финал для 10 класса впервые прошёл в 2015 году, а для 9 класса — в 2016 году.

Письменный экзамен мехмата МГУ и ДВИ МГУ

Мехмат	, , , , , 04-03, 04-07;  03-03, 03-05, 03-0702-03, 02-05, 02-07;  01-03, 01-05, 01-0700-03, 00-05, 00-07;  99-03, 99-05, 99-0798-03, 98-05, 98-07;  97-03, 97-05, 97-0796-03, 96-05, 96-07;  95-03, 95-05, 95-0794-05, 94-07, 93-05, 93-07
ДВИ	, , , , , , ,