Главные формулы для егэ по профильной математике

Формулы по базовой математике для ЕГЭ

Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:

• таблица квадратных чисел от 0 до 99;
• свойства арифметического квадратного корня;
• формулы сокращенного умножения;
• корни квадратного уравнения;
• свойства степени и логарифма;
• теорема Пифагора;
• формула расчета длины окружности и площади круга;
• расчет средней линии треугольника и трапеции;
• радиус вписанной и описанной окружности правильного треугольника;
• формулы расчета площади планиметрических фигур;
• вычисление поверхностей и объемов тел;
• основные тригонометрические функции и тождества;
• график линейной функции;
• геометрический смысл производной.

Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.

Дробно рациональные уравнения

• Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
• Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. Найти общий знаменатель дробей, входящих в уравнение;
3. Умножить обе части уравнения на общий знаменатель;
4. Решить получившееся целое уравнение;
5. Исключить из его корней те, которые не удовлетворяют условию ОДЗ.

Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения

Тригонометрия

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Формулы приведения задаются в виде таблицы:

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

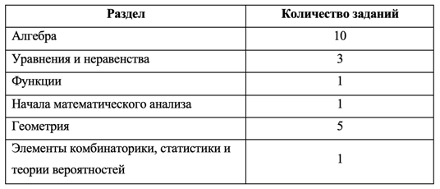
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Теория к заданию 4 из ЕГЭ по математике (профильной)

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}{-}$.

$Р(А)+Р{(А)}{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Формулы для базового ЕГЭ-2022 по математике

Формулы сокращённого умножения

`(a + b)^2=a^2 + 2ab + b^2`
`(a − b)^2=a^2 − 2ab + b^2`
`a^2 − b^2=(a + b)(a − b)`
`a^3 + b^3=(a + b)(a^2 − ab + b^2)`
`a^3 − b^3=(a − b)(a^2 + ab + b^2)`
`(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3`	Эти две формулы заучивать не обязательно, но желательно
`(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3`

Прогрессии

Геометрическая прогрессия:

`b_n=b_(n-1)*q`

`b_n=b_1*q^(n-1)`

`S_n=((q^n-1)*b_1)/(q-1)`

Бесконечно убывающая: `S=b_1/(1-q)`

Вероятность

Вероятность события A:	`P(A)=m/n`	m — число благоприятных событийn — общее число событий
События происходят A и B происходят одновременно	`A*B`
Независимые события:	`P(A*B)=P(A)*P(B)`	Когда вероятность одного события (А) не зависит от другого события (B)
Зависимые события:	`P(A*B)=P(A)*P(B|A)`	`P(B|A)` — вероятность события B при условии, что событие A наступило
Происходит или событие A, или B	`A+B`
Несовместные события:	`P(A+B)=P(A)+P(B)`	Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0`
Совместные события:	`P(A+B)=P(A)+P(B)-P(A*B)`	Когда оба события могут наступить одновременно

Свойства степеней

`a^0=1`	`a^1=a`
`a^(-1)=1/a`	`a^(-n)=1/a^n`
`a^(1/2)=sqrt(a)`	`a^(1/n)=root(n)(a)`
`a^m*a^n=a^(m+n)`	`a^m/a^n=a^(m-n)`
`(a*b)^n=a^n*b^n`	`(a/b)^n=a^n/b^n`
`(a^m)^n=a^(m*n)`	`a^(m/n)=root(n)(a^m)`

Свойства логарифмов

`log_ab=c«a^c=b`	Определение логарифма
`log_a1=0`
`log_aa=1`
`log_a(b*c)=log_ab+log_ac`
`log_a(b/c)=log_ab-log_ac`
`log_ab^n=n*log_ab`
`log_(a^m)b=1/m*log_ab`
`log_ab=1/(log_ba)`
`log_ab=(log_cb)/(log_ca)`
`a^(log_cb)=b^(log_ca)`
`a^(log_ab)=b`

Геометрия

Планиметрия (2D)

Тригонометрия:	`sinA=a/c`   `cosA=b/c`
	`text(tg)A=sinA/cosA=a/b`
Теорема косинусов:	`c^2=a^2+b^2-2ab*cosC`
Теорема синусов:	`a/sinA=b/sinB=c/sinC=2R`	где R — радиус описанной окружности
Уравнение окружности:	`(x-x_0)^2+(y-y_0)^2=R^2`	где `(x_0;y_0)` — координаты центра окружности
Соотношение вписанного и центрального углов:	`beta=alpha/2=(uualpha)/2`
Описанная окружность, треугольник:	`R=(abc)/(4S)`		См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров.
Вписанная окружность, треугольник:	`r=S/p`		где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис.
Описанная окружность, четырёхугольник:	`alpha+gamma=beta+delta=180^circ`
Вписанная окружность, четырёхугольник:	`a+c=b+d`
Свойство биссектрисы:	`a/x=b/y`
Теорема о пересекающихся хордах:	`AM*BM=CM*DM`		Эти теоремы необходимо уметь выводить
Теорема об угле между касательной и хордой:	`alpha=1/2uuAB`
Теорема о касательной и секущей:	`CM^2=AM*BM`
Теорема об отрезках касательных:	`AB=AC`

Площади фигур:

Окружность:	`S=pir^2`
Треугольник:	`S=1/2ah`
Параллелограмм:	`S=ah`
Четырёхугольник:	`S=1/2d_1d_2sinvarphi`	У ромба `varphi=90^@`
Трапеция:	`S=(a+b)/2*h`

Обратные тригонометрические функции и простейшие тригонометрические уравнения

Арккосинус

Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.

Если, $|а|≤1$, то $arccos а = t ⇔ \{\table \cos (t)=a; \0≤t≤π;$

$arcos(-a) = π-arccos⁡a$, где $0≤а≤1$

Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение

$t=±arccos ⁡ a+2πk; k∈Z$

Частные случаи

$cos t =1, t = 2πk;k∈Z$

$cos t = 0, t = {π}/{2}+πk;k∈Z$

$cos t = -1, t=π+2πk;k∈Z$

Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$

$сos{2πx}/{3}=-{√3}/{2}$

${2πx}/{3}=±arccos⁡(-{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$

${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$

${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$

Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$

$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$

$x=±1,25+3k$

Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения

$k=0$

$x_1= -1,25$

$x_2=1,25$

$к=1$

$х_1=3-1,25=1,75$

$х_2=3+1,25=4,25$

Нам подходит $1,25$ – это и есть результат

Ответ: $1,25$

Арксинус

Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.

Если, $|а|≤1$, то $arcsin a = t ⇔ \{\table \sint=a; \-{π}/{2}≤t≤{π}/{2};$

$arcsin(-a)= — arcsin a$, где $0≤а≤1$

Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:

$1. t_1 = arcsin a+2πk;k∈Z$

$t_2 = (π- arcsin a)+ 2πk;k∈Z$

$2. t=(-1)^n arcsin ⁡ a+πn; n∈Z$

$3.$ Частные случаи

$sin t = 0, t=πk;k∈Z$

$sin t = 1, t={π}/{2}+2πk;k∈Z$

$sin t = -1,t=-{π}/{2}+2πk;k∈Z$

Арктангенс

$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.

$arctg a = t ⇔ \{\table \tgt=a; \-{π}/{2}≤t≤{π}/{2};$

$arctg(-a)= — arctg a$

Основные формулы для профильного ЕГЭ

Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.

Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:

• правила сокращенного умножения;
• арифметическая и геометрическая прогрессии;
• основы вероятностной теории;
• свойства степеней и логарифмов;
• азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
• производная (правила дифференцирования, элементарнее функции и уравнение касательной);
• первообразная;
• двухмерная планиметрия;
• правила нахождения площадей геометрических фигур;
• трехмерная стереометрия.

Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:

1. ЕГЭ по математике – формулы для алгебры и начал анализа
2. Формулы ЕГЭ – математика, раздел геометрия

Материалы для скачивания – в формате pdf.

Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Формулы для ОГЭ-2022 по математике

Формулы сокращённого умножения

`(a + b)^2=a^2 + 2ab + b^2`
`(a − b)^2=a^2 − 2ab + b^2`
`a^2 − b^2=(a + b)(a − b)`
`a^3 + b^3=(a + b)(a^2 − ab + b^2)`
`a^3 − b^3=(a − b)(a^2 + ab + b^2)`
`(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3`	Эти две формулы заучивать не обязательно, но желательно
`(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3`

Прогрессии

Геометрическая прогрессия:

`b_n=b_(n-1)*q`

`b_n=b_1*q^(n-1)`

`S_n=((q^n-1)*b_1)/(q-1)`

Бесконечно убывающая: `S=b_1/(1-q)`

Вероятность

Вероятность события A:	`P(A)=m/n`	m — число благоприятных событийn — общее число событий
События происходят A и B происходят одновременно	`A*B`
Независимые события:	`P(A*B)=P(A)*P(B)`	Когда вероятность одного события (А) не зависит от другого события (B)
Зависимые события:	`P(A*B)=P(A)*P(B|A)`	`P(B|A)` — вероятность события B при условии, что событие A наступило
Происходит или событие A, или B	`A+B`
Несовместные события:	`P(A+B)=P(A)+P(B)`	Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0`
Совместные события:	`P(A+B)=P(A)+P(B)-P(A*B)`	Когда оба события могут наступить одновременно

Свойства степеней

`a^0=1`	`a^1=a`
`a^(-1)=1/a`	`a^(-n)=1/a^n`
`a^(1/2)=sqrt(a)`	`a^(1/n)=root(n)(a)`
`a^m*a^n=a^(m+n)`	`a^m/a^n=a^(m-n)`
`(a*b)^n=a^n*b^n`	`(a/b)^n=a^n/b^n`
`(a^m)^n=a^(m*n)`	`a^(m/n)=root(n)(a^m)`

Геометрия

Планиметрия (2D)

Тригонометрия:	`sinA=a/c`   `cosA=b/c`
	`text(tg)A=sinA/cosA=a/b`
Теорема косинусов:	`c^2=a^2+b^2-2ab*cosC`
Теорема синусов:	`a/sinA=b/sinB=c/sinC=2R`	где R — радиус описанной окружности
Уравнение окружности:	`(x-x_0)^2+(y-y_0)^2=R^2`	где `(x_0;y_0)` — координаты центра окружности
Соотношение вписанного и центрального углов:	`beta=alpha/2=(uualpha)/2`
Описанная окружность, треугольник:	`R=(abc)/(4S)`		См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров.
Вписанная окружность, треугольник:	`r=S/p`		где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис.
Описанная окружность, четырёхугольник:	`alpha+gamma=beta+delta=180^circ`
Вписанная окружность, четырёхугольник:	`a+c=b+d`
Свойство биссектрисы:	`a/x=b/y`
Теорема о пересекающихся хордах:	`AM*BM=CM*DM`		Эти теоремы необходимо уметь выводить
Теорема об угле между касательной и хордой:	`alpha=1/2uuAB`
Теорема о касательной и секущей:	`CM^2=AM*BM`
Теорема об отрезках касательных:	`AB=AC`

Площади фигур:

Применение формул сокращенного умножения

1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.

$(a+b)^2=a^2+2ab+b^2$

2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

$(a-b)^2=a^2-2ab+b^2$

3. Разность квадратов раскладывается на произведение разности чисел и их сумму.

$a^2-b^2=(a+b)(a-b)$

4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.

$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.

$a^3+b^3=(a+b)(a^2-ab+b^2)$

7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.

$a^3-b^3=(a-b)(a^2+ab+b^2)$

Задача №17, экономическая

Стандартное начало условия:

• 1-го числа каждого месяца долг возрастает на `color(green)(r%)`.
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга.
• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Основная идея решения:

1. каждый месяц (15-го числа) долг должен уменьшаться на одну и ту же величину, т.е. на `1/n` часть изначального долга, т.е. на `color(blue)(S/n)`
2. каждый месяц (1-го числа) банк увеличивает остаток долга на `color(green)(r%)`.
3. каждый месяц (2-14-го числа) клиент выплачивает начисленные проценты (пункт 2) и ежемесячную часть долга (пункт 1).

Составляем таблицу платежей по месяцам:

Взятие кредита:
15 декабря:	Долг = `S` рублей.
1-й месяц:
1 января	Банк начисляет проценты = `color(green)(S*r)`
	Долг = `S + color(green)(S*r)`
2-14 января	Платим `color(green)(S*r) + color(blue)(S/n)`
	Долг = « `– [ color(green)(S*r) + color(blue)(S/n) ] = S-color(blue)(S/n) = (n-1)/n*S`
2-й месяц:
1 февраля	Банк начисляет проценты = `color(green)(obrace((n-1)/n*S)^(«Предыд.долг»)*r)`
	Долг = `(n-1)/n*S+` `color(green)((n-1)/n*S*r)`
2-14 февраля	Платим `color(green)((n-1)/n*S*r)+` `color(blue)(S/n)`
	Долг = `[(n-1)/n*S +` `color(green)((n-1)/n*S*r)]–` `[color(green)((n-1)/n*S*r)+` `color(blue)(S/n)]=` `(n-1)/n*S — color(blue)(S/n)=` `(n-2)/n*S`
3-й месяц:
1 марта	Банк начисляет проценты = `color(green)((n-2)/n*S*r)`
	Долг = `(n-2)/n*S + color(green)((n-2)/n*S*r)`
2-14 марта	Платим `color(green)((n-2)/n*S*r) + color(blue)(S/n)`
	Долг = `[(n-2)/n*S + color(green)((n-2)/n*S*r)] – [color(green)((n-2)/n*S*r) + color(blue)(S/n)] = (n-2)/n*S — color(blue)(S/n) = (n-3)/n*S`
(n-1)-й месяц:	Остаток долга = `2/n*S`
1 мартобря	Банк начисляет проценты = `color(green)(2/n*S*r)`
	Долг = `2/n*S + color(green)(2/n*S*r)`
2-14 мартобря	Платим `color(green)(2/n*S*r) + color(blue)(S/n)`
	Долг = `[2/n*S + color(green)(2/n*S*r)] – [color(green)(2/n*S*r) + color(blue)(S/n)] = 2/n*S — color(blue)(S/n) = 1/n*S`
n-й месяц:	Остаток долга = `1/n*S`
1 апребря	Банк начисляет проценты = `color(green)(1/n*S*r)`
	Долг = `1/n*S + color(green)(1/n*S*r)`
2-14 апребря	Платим `color(green)(1/n*S*r) + color(blue)(S/n)`
	Долг = `[1/n*S + color(green)(1/n*S*r)] – [color(green)(1/n*S*r) + color(blue)(S/n)] = 1/n*S — color(blue)(S/n) = 0`